У Моисеев В.И., 1999

Философия, по нашему мнению, достаточно регулярно использует следующие логические конструкции. Вводится, во-первых, некоторое начало Х, и, во-вторых, некоторое множество элементов У₁, У₂, …, Уn рассматривается как множество “сторон”, “аспектов”, “мод” начала Х, образованных как условные виды бытия Х – как существования Х при некоторых условиях Z₁, Z₂, …, Z_n. Таким образом, каждое Уi – это “Х-при-некотором-условии-Zi”, i=1,2,..,n. Тем самым происходит возведение множества из независимых друг от друга элементов Уi к “усовершенному” или “преображенному” множеству “мод” “Х-при-некотором-условии-Zi”, в котором все ранее независимые начала оказываются сторонами-аспектами единого “высшего” начала Х. Такого рода ментальную технику можно рассматривать как наиболее общее выражение различных частных процедур синтеза, столь характерных именно для философского знания. В качестве примеров подобной техники можно, например, указать на метод философского познания первоначал бытия (идей), описываемый Платоном в диалоге “Парменид”, на представление определенностей как модусов и атрибутов субстанции в философии Спинозы, этапов развития абсолютной идеи в философии Гегеля, предикаций сущего в философии всеединства у Соловьева, и т.д. Такие процедуры “возведения к единству” присущи не только монистической традиции философии, но и разного рода плюралистическим направлениям (элементаризм Эпикура и Анаксагора, дуализм Декарта, и т.д.). В этом случае синтез выражается в возведении множества начал У₁, У₂, …, Уn не к одному основанию, но к множеству подобных оснований – Х₁, Х₂, …, Хm. В этом случае синтетичность выражается в существенном уменьшении разнообразия оснований по сравнению с разнообразием возводимых к единству начал (m<n).

Обобщая подобного рода синтетические техники, мы вводим понятие особой математической структуры – “ментального многообразия”. Начала Х₁, Х₂, …, Хm, к которым происходит возведение, мы называем “модусами”, те системы условий Z₁, Z₂, …, Zn, при которых проявляют себя модусы как конкретные начала, мы называем “моделями”, а сами конкретные начала У₁, У₂, …, Уn, представленные как условное бытие какого-либо модуса Хj, j=1,2,…,m, при какой-либо модели Zi, мы называем “модами”, и обозначаем их как ХjЇ Zi – “Хj-при-некотором-условии-Zi”. Операцию Ї мы называем операцией “проецирования”, рассматривая модусы как своего рода “проекции” модусов в моделях. Ниже дается более строгое определение ментального многообразия в терминах теоретико-множественного подхода.

Определение. Ментальным многообразием будем называть четверку

e = <М₁,М₂,М₃,Ї >, где

М₁ - непустое множество объектов, называемых “модусами”,

М₂ - непустое множество объектов, называемых “моделями”,

М₃ - непустое множество объектов, называемых “модами”,

Ї - операция проецирования.

Будем обозначать элементы М₁ через М, элементы М₂ – через m, элементы М₃ – через m .

Для каждого модуса М введем множества:

М₂(М) – множество моделей (подмножество М₂), поставленных в соответствие модусу М (множество моделей модуса М),

М₃(М) – множество мод (подмножество М₃) модуса М.

В этом случае операцию проецирования Ї будем понимать как множество биективных отображений Ї _М: {М}ґ М₂(М)® М₃(М), т.е элементы М₃(М) – это в точности множество элементов вида Ї _М(М,m) = МЇ _Мm, где mО М₂(М). Положим: МЇ m=МЇ _Мm, где mО М₂(М).

Т.о. каждая мода m может быть представлена в виде МЇ m – “модус М при условии модели m” (“проекция модуса М в рамках модели m”).

Положим, что М₂ – это объединение М₂(М) по всем МО М₁, М₃ – объединение М₃(М) по всем МО М₁.

Для каждой модели m могут быть определены множества М₃(m) – множество мод вида МЇ m, где варьирует переменная М, и М₁(m) – множество модусов с ненулевым пересечением множеств М₂(М) и {m}(возможен подход, при котором модус M отождествляется с множеством М₃(M ), модель m – с множеством М₃(m)). Мы полагаем также, что для каждого М₃(m) определено отношение эквивалентности =_m – “равенство в модели m”.

Пару <М,М₃(М)> будем называть полнотой (определения) модуса М и обозначать через p М (это модус вместе со своими модами).

Пару <m,М₃(m)> будем называть полнотой (определения) модели m и обозначать через p m (это модель вместе со своими модами).

Если для каждого модуса М определено некоторое непустое подмножество “канонических моделей М”, М₂^К(М), множества М₂(М), то такое ментальное многообразие будем называть каноническим (идея “каноничности” модели может быть проинтерпретирована как условия моделирования модуса, наиболее адекватно выражающие природу этого модуса с той или иной точки зрения. В общем случае эта интерпретация зависит от конкретного вида ментального многообразия, и в рамках формальных определений мы только отмечаем такую возможность). Моду МЇ m, где mО М₂^К(М), будем в этом случае называть К-статусом модуса М, а канонические модели (К-модели) для модуса М в этом случае будем обозначать через mМ.

Если множество М₂^К(М) состоит из одного элемента для каждого модуса М, то такое ментальное многообразие будем называть 1-каноническим

Ментальное многообразие будем называть регулярным, если оно 1-каноническое, М₂(М)=М₂ для любого модуса М, и между модусами и их К-моделями установлена биекция.

Если на М₃(m) введено отношение порядка, m*=mМ* (т.е. m* – это К-модель для модуса М*), и выполнено свойство МЇ m*Ј М*Ї m* для любого модуса М (где равенство понимается в смысле равенства в модели m*), то такое ментальное многообразие будем называть ментальным многообразием с каноническим доминированием (это означает, что множество мод МЇ m* в модели m*оказываются подчиненными канонической моде М*Ї m*, т.е. эта мода доминирует относительно введенного порядка). Если МЇ m*=М*Ї m* (здесь имеется в виду равенство в модели m*), то будем говорить, что модус М дан в L-статусе в модели m*. В противном случае, т.е. если МЇ m* < М*Ї m*, то будем говорить, что модус М дан в М-статусе в модели m*. Ясно, что если модус дан в К-статусе в модели m (в рамках ментального многобразия с каноническим доминированием), то он дан в L-статусе в этой модели. L- и М-статусы будем называть R-статусами.

М₁ < М₂ ® М_1Ї m₁ = М_2Ї m₁, где m₁ – это К-модель для модуса М₁ и равенство понимается как равенство в модели m₁, то такое ментальное многообразие будем называть экранирующим ментальным многообразием.

(M ₁ * M ₂ )Ї M ₃ = M _{1Ї M 3} * M _{2Ї M 3},

где M ₁, M ₂, M ₃ - любые три модуса,

* - операции пересечения (З ) или объединения (И ), и

(щ M )Ї M ’ = щ (M Ї M ’),

то такие ментальные многообразия можно называть правильными булевыми.

В уже упоминавшемся диалоге “Парменид” Платона мы находим описание следующего метода. Устами Парменида Платон говорит: “Если ты желаешь поупражняться, то возьми хотя бы предположение, высказанное Зеноном: допусти, что существует многое, и посмотри, что должно из этого вытекать как для многого самого по себе в отношении к самому себе и к единому, так и для единого в отношении к самому себе и ко многому. С другой стороны, если многого не существует, то опять надо смотреть, что последует отсюда для единого и для многого в отношении их к себе самим и друг к другу… одним словом, что только ни предположишь ты существующим или несуществующим, или испытывающим какое-либо иное состояние, всякий раз должно рассматривать следствия как по отношению к этому предположению, так и по отношению к прочим, взятым поодиночке, и точно так же, когда они в большем числе или в совокупности. С другой стороны, это прочее тебе тоже следует всегда рассматривать в отношении как к нему самому, так и к другому, на чем бы ты ни остановил свой выбор и как бы ты ни предположил то, что предположил существующим или несуществующим, если ты хочешь, поупражнявшись надлежащим образом в этих вещах, основательно прозреть истину” (3, С.358-359). Таким образом, здесь Платон разъясняет метод некоторого закономерного варьирования того или иного понятия в рамках определенной системы отношений. Такое варьирование можно проинтерпретировать в терминах ментального многообразия как взятие мод понятия-модуса при тех или иных условиях (моделях). Пусть Х – некоторое понятие. Тогда, во-первых, Х может браться при условиях своего существования (В) – как мода ХЇ В, и при условиях своего несуществования (щ В) – как мода ХЇ щ В (очевидно, то же можно сделать и по отношению к щ Х – отрицанию Х). Во-вторых, понятие Х может также рассматриваться в отношении к себе, обозначим это в виде “рефлексивной” моды ХЇ Х, и в отношении к своему иному (щ Х) – обозначим такую “трансфлексивную” моду через ХЇ щ Х. Кроме того, иное к Х (щ Х) также может быть рассмотрено в отношении к себе (щ ХЇ щ Х), и в отношении к своему иному, т.е. к Х=щ щ Х, т.е. как мода щ ХЇ Х. Теперь описываемый Платоном метод может быть представлен в седующем виде. Моды ХЇ В и ХЇ щ В берутся как модели в некотором новом ментальном многообразии, а в качестве модусов этого многообразия берутся моды ХЇ Х, ХЇ щ Х, щ ХЇ Х и щ ХЇ щ Х. Каждый модус здесь может образовать моду при каждой модели, т.е. в целом здесь для каждого модуса возникает по две моды, а так как модусов четыре, то всего возникает восемь мод – это как раз число частей в диалоге “Парменид”.

Итак, по сути дела описанным методом предполагаются три ментальных многообразия – e ₁,e ₂ и e ₃. Именно:

e ₁ = <М₁₁,М₂₁,М₃₁,Ї >,

где М₁₁= { Х, щ Х }- множество модусов,

М₂₁= {B, щ B} – множество моделей,

М₃₁= {XЇ B, XЇ щ B, щ XЇ B, щ XЇ щ B}- множество мод.

e ₂ = <М₁₂,М₂₂,М₃₂,Ї >,

где М₁₂= { Х, щ Х }- множество модусов,

М₂₂= {Х, щ Х} – множество моделей,

М₃₂= {XЇ Х, XЇ щ Х, щ XЇ Х, щ XЇ щ Х}- множество мод.

e ₃ = <М₁₃,М₂₃,М₃₃,Ї >,

где М₁₃= { XЇ Х, XЇ щ Х, щ XЇ Х, щ XЇ щ Х }- множество модусов,

М₂₃= { ХЇ В, ХЇ щ В } – множество моделей,

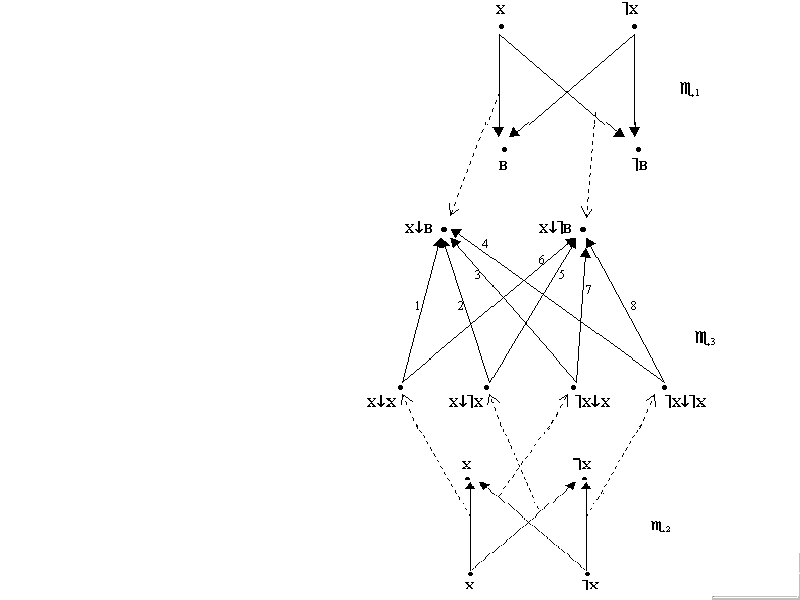
М₃₃={(XЇ Х)Ї (XЇ B), (XЇ Х)Ї (XЇ щ B), (XЇ щ Х)Ї (XЇ B), (XЇ щ Х)Ї (XЇ щ B), (щ XЇ Х)Ї (ХЇ В), (щ XЇ Х)Ї (ХЇ щ В), (щ XЇ щ Х)Ї (ХЇ В), (щ XЇ щ Х)Ї (ХЇ щ В) }- множество мод.

Рис.1. Структура ментальных многообразий в диалоге “Парменид” Платона. Здесь стрелка от А к В означает моду АЇ В. Если Х = Е (“единое”) и щ Х = щ Е (“не-единое” = “многое”), то получим моды в ментальном многообразии e ₃ (они изображены стрелками), составляющие логическую формулу каждой из восьми частей диалога “Парменид” Платона (нумерация у стрелок соответствует в этом случае нумерации частей диалога).

Все описанные ментальные многообразия таковы, что здесь М_2i(М)=М_2i , где i=1,2,3. Для второго ментального многообразия модели, равные модусам, можно определить как канонические модели, в связи с чем это ментальное многообразие может быть определено как регулярное, и рефлексивные моды ХЇ Х и щ ХЇ щ Х – это К-статусы модусов Х и щ Х соотв. Например, “единое-в-отношении-к-себе”, как мода ЕЇ Е, - это рассмотрение “единого” в своей канонической модели. Обобщение описанного метода связано с тем, что 1)кроме категорий бытия (В) и небытия (щ В), могут рассматриваться другие предикации Х, 2)в качестве иного к Х могут рассматриваться все возможные подмножества множества некоторых начал Х₁, Х₂, …, Хk.

1. Моисеев В.И., Чусов А.В. О разнообразии статусов существования и модальности предельных понятий// Вестник МГУ. Серия 7. Философия, № 4, 1997. - С. 82 - 104.